The Skeptics Society & Skeptic magazine

Leonardo da Vinci was a man of many talents. He was one of the few individuals to have made contributions to both the arts and science. His work extends to civil engineering, chemistry, geology, geometry, hydrodynamics, mathematics, mechanical engineering, optics, physics, pyrotechnics, warfare, and zoology.

Da Vinci was one of the best artists of his generation and many of his paintings are greatly admired today and command astronomical prices (his Salvator Mundi fetched the highest auction price ever). He was also an extraordinary illustrator, leaving thousands of manuscripts full of drawings of machines, fluid mechanics, humans, and many other topics. In addition, he was also a sculptor, architect, and more. As the type specimen of a Renaissance man, he put his mind to many different subjects, and he excelled at most of them. He was generally considered a genius by his contemporaries. In addition to all of this, he was described as a handsome and charming man, who was able to convince a whole room of the feasibility of something impossible.¹ However, as it is sometimes said of promising but lazy children, some said that he would have been capable of even more accomplishments had he put his focus on them for longer and worked harder.

Revealingly, in his time, Leonardo was not considered to be at the same level as Michelangelo or even Raphael, perhaps because his notebooks were not published until much later. However, today many consider him superior to all his peers and—in a few extreme cases—some people fall into what we might call the “cult of Leonardo,” whose adherents believe that his genius was almost superhuman.

Consider a recently published article titled “Leonardo da Vinci’s Visualization of Gravity as a Form of Acceleration” by Morteza Gharib, Chris Roh, and Flavio Noca (henceforth GRN).² In it, the authors propose that Leonardo understood gravity in a way that was not surpassed until the works of Galileo, Newton, and even Einstein. Had GRN presented their ideas in a less spectacular way, their article could have been a flawed, but mainly harmless one. Unfortunately, they chose to take the more risky path of venturing unfounded, under-researched, mind-blowing claims under the guise of solid scholarship, starting with the assertion that Leonardo saw gravity not as a force, but as an acceleration:

About 500 years ago, Leonardo da Vinci tried to uncover the mystery of gravity and its connection to acceleration through a series of ingenious experiments guided only by his imagination and masterful experimental techniques.

The shocking revelation that they put forth is that Leonardo “almost” (bit of wiggle room there) anticipated Einstein’s General Theory of Relativity, in particular, the so-called “Equivalence Principle” (see Figure 1):

As with Galileo, Leonardo’s geometrical representation of the equation of motion is as insightful as Newtonian mechanics’ representations of equations of motion. […] After Newton, Albert Einstein referred to the equivalency of gravity and acceleration, when he introduced the principles of “strong equivalency” while developing his theory of relativity in the early twentieth century.

Figure 1. (Click image to enlarge) Einstein’s equivalence principle states that gravity is indistinguishable from being in an accelerated system of reference. This was famously illustrated by Einstein using a thought experiment: imagine we are in a closed room. Is there any way we can know if the down force that we feel is due to gravity? Maybe the room is in a spaceship, away from big masses and accelerating upwards with acceleration g. Einstein concluded that both situations are equivalent.

Considering gravity as an acceleration instead of a force is indeed a crucial difference between Einstein’s and Newton’s conceptions. The assertion that Leonardo could have hit upon this insight centuries before Einstein is the most preposterous claim in GRN’s article and likely what has made it so ballyhooed in the popular press. To give just a couple of examples of some of those reviews, here is one from Ars Technica:

[Leonardo attempted] to draw a link between gravity and acceleration—well before Isaac Newton came up with his laws of motion, and centuries before Albert Einstein would demonstrate the equivalence principle with his general theory of relativity.³

Here’s another one from CNET:

Before Galileo, Newton, and Einstein, it seems to be Leonardo da Vinci who started piecing together the gravity puzzle […] Rather, it’s kind of the same thing as acceleration…. [Einstein] called it the equivalence principle, and soon, this eye-opening concept would blossom into the mind-bending theory of general relativity. The rest, as they say, is history.⁴

Let’s summarize GRN’s argument. First, they assert that Leonardo had a good understanding of how objects fall with constant acceleration under the effect of gravity. Second, they present a thought experiment devised by Leonardo that, they claim, shows he understood that gravity is equivalent to being in an accelerated frame of reference. Finally, they present a quantitative model, purportedly based on Leonardo’s manuscripts, and they compare it against Newtonian mechanics. Let’s consider each of these points.

Acceleration of Falling Objects

To support their claim that Leonardo understood that gravity produces a constant acceleration on falling objects, GRN provide the following quote from Leonardo’s M manuscript: “a weight that descends freely in every degree of time acquires…a degree of velocity”⁵ (ellipsis in their article). They further tell us that “many scholars of Leonardo note that this statement indicates that Leonardo correctly understood that the velocity of a falling object is a linear function of time.”

Now consider Leonardo’s quote in full: “The free-falling body acquires a degree of displacement over each degree of time, and over each degree of displacement it acquires a degree of velocity.”⁶ It is not completely clear what Leonardo meant by this, since the original sentence can be translated in slightly different ways; but the simplest interpretation is that Leonardo didn’t have a full understanding of acceleration. He repeats similar ideas in various places,⁷ including in drawings and calculations.⁸ For the full quote, I have used a translation from Prof. Enzo Macagno, one of the scholars that GRN cite in support of their hypothesis. Macagno has this to say about Leonardo’s understanding of gravity relative to this quote:

what Leonardo is trying to express is that over equal intervals of time there are constant increments for both distance traversed and for velocity. If this is understood, we may study critically what Leonardo said to detect how far he went in his descriptions of motion during free fall. Even if he did not add anything new to this question, or actually detracted from it, it is still important to know his “degree” of understanding.⁹

However, Macagno then notes that, “In his descriptions of an accelerated motion, which could not be correct because of an intrinsic inconsistency between velocity and displacement,” an observation that is hardly in support of GRN’s claim.

Another point to consider is the concept of “free fall.” Today we apply it to objects moving exclusively under the influence of the Earth’s gravity. However, when Leonardo talks about free fall (“discienso libero”), he was probably referring to something different. Da Vinci was very conscious of the effect of air drag. In almost every case where he talks about falling objects, he mentions the effect of air and he even includes it in his simplified calculations.¹⁰ In his manuscripts, he has many things to say about the effect of air on falling objects and vice versa. To me, it is much more likely that for Leonardo, free fall meant something closer to what we now call “terminal velocity”— that is, that constant velocity which a falling object reaches due to the balance between gravity and air resistance.

Further, Leonardo mentions several times that, on sunny clear days, the air is lighter at higher altitudes, so that the air becomes thicker as the object falls. This means that he thought that, at terminal velocity, objects decelerate as they fall. This is actually true, although the effect is probably much weaker than what Leonardo implies. None of these considerations discussed at length by Da Vinci in his manuscripts are mentioned in GRN’s article.

Leonardo’s Thought Experiment

Having argued that Leonardo thought that objects fell with constant acceleration, the next step in GRN’s article is to “prove” that Leonardo had a deeper understanding, namely that he was somehow aware that gravitation was not a force, but an acceleration in a manner similar to Einstein’s equivalence principle (see Figure 1). To do this, GRN analyze a thought experiment that Leonardo described in slightly different forms in various parts of his manuscripts.

Figure 2. Leonardo’s thought experiment. The jar moves from left to right releasing beads as it moves (Manuscript M, 143r).

The experiment consists of an open “container” (a jar, a funnel, and even a cloud in his various descriptions) that moves horizontally as it allows some particles to fall (beads or hail grains). Leonardo then considers the geometry of the system, giving special consideration to the case where the jar moves horizontally at the same speed as the first released bead falls vertically. This can be seen in Figure 2 as drawn by Leonardo, where he explains that, in this particular case, the trajectory of the first bead, the one of the jar, and the line that connects all beads, form an isosceles right triangle.

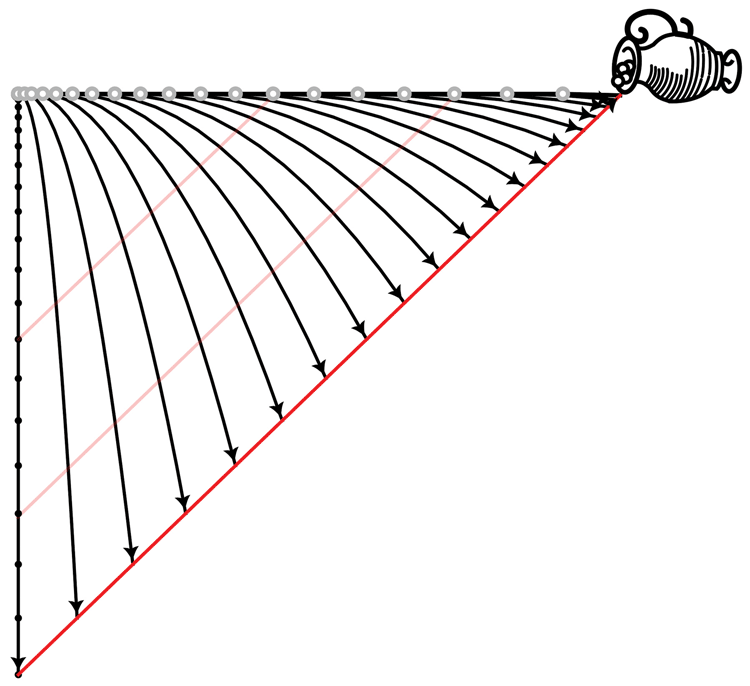
Figure 3. GRN’s interpretation of the experiment. All movements are accelerated, and the beads follow parabolas.

GRN analyze this problem using a more modern Newtonian approach. As is commonly done in high school physics problems, they start by simplifying away the effect of the air—an unusual assumption in this case—given that Leonardo constantly talks about the effect of air on falling objects. They also use the perhaps more reasonable assumption that particles leave the jar at the same speed as the jar itself, not considering that they must be moving with some relative speed out of it. They show their results in a graphic similar to Figure 3.

Figure 2 is not identical to the one drawn by Leonardo, but some salient features are still there: an isosceles right triangle, abn, defined by the movement of the jar (an), the falling trajectory of the first bead (ab), and the straight line that connects all the beads (bn). GRN assert that this is what Leonardo had in mind and they use the fact that, in both cases, the line formed by the falling beads is a straight line as proof that their assumptions are correct. They contrast it against the case in which the jar moved at constant velocity while the beads fall accelerated by gravity, in which case the beads align, but in a vertical line. They never entertain the more logical possibility: that Leonardo thought that the beads fell vertically at more or less constant velocities.

Then GRN go on to explain that this system can be better understood from the point of view of the accelerated frame of reference of the moving jar, a technique not available in Leonardo’s time but in the toolbox of Newtonian mechanics. Probably, they do this to remind us of Einstein’s Equivalence Principle, wherein the connection between gravity and acceleration is deeper and where accelerated frames of reference are equivalent to gravity fields. To me, it is clear that GRN’s ulterior and ultimate motivation is to establish a connection with the General Theory of Relativity. Throughout the article they leave small hints of this; for example, they say that “Leonardo’s studies of objects in free fall demonstrate that gravitational and pseudo-acceleration fields are indistinguishable locally when their magnitudes are the same.” Here, the words “fields” and “indistinguishable locally” have nothing to do with anything Leonardo writes, but GRN say it anyway because it is a language that feels more Einsteinian. In another part of the article, they say: “in other words, he [Leonardo] switched time with space to be able to conduct this experiment,” which is a thinly veiled way of suggesting that Leonardo was wise to the space-time continuum.

Of course, Einstein’s Equivalence Principle is deeper than just comparing accelerations. That could have been done in Newtonian mechanics. The crucial point that Einstein understood is that the mass of an object subjected to a gravitational field plays no role in its dynamics. All objects are accelerated equally, even light! Leonardo never says that all objects fall at the same speed independently of their weight; quite the contrary. Leonardo gives various examples where they don’t, although he mentions air resistance as one reason. Famously, Galileo was the first person to prove that all objects fall at the same speed (not including the effect of air), and there is no reason to believe that Leonardo knew that before Galileo.

Figure 4. Leonardo’s Manuscript M 217r (left), and my translation (right). The image above has been mirrored from the original for ease of understanding. Leonardo wrote from right to left, using his left hand, to prevent smudging the ink as he wrote.

I have translated the page where Leonardo presents the experiment of the hail cloud (see Figure 4). My translation is quite literal, except that I have simplified the third paragraph which, to me, was a little bit reiterative and confusing. It is clear that Leonardo thought that hail grains fell mostly vertically, without any appreciable horizontal velocity, as indicated by the vertical lines that connect every grain with the location at the moment it was released. Leonardo thought that the effect of the air would make objects quickly stop any horizontal movement (see Figure 5). The fact that he also thought that this experiment could be performed substantiates the assumption that he was considering objects falling at constant velocity. Should we believe Leonardo was thinking that clouds could be seen accelerating to absurdly great speeds or that hail grains were not affected by air resistance?

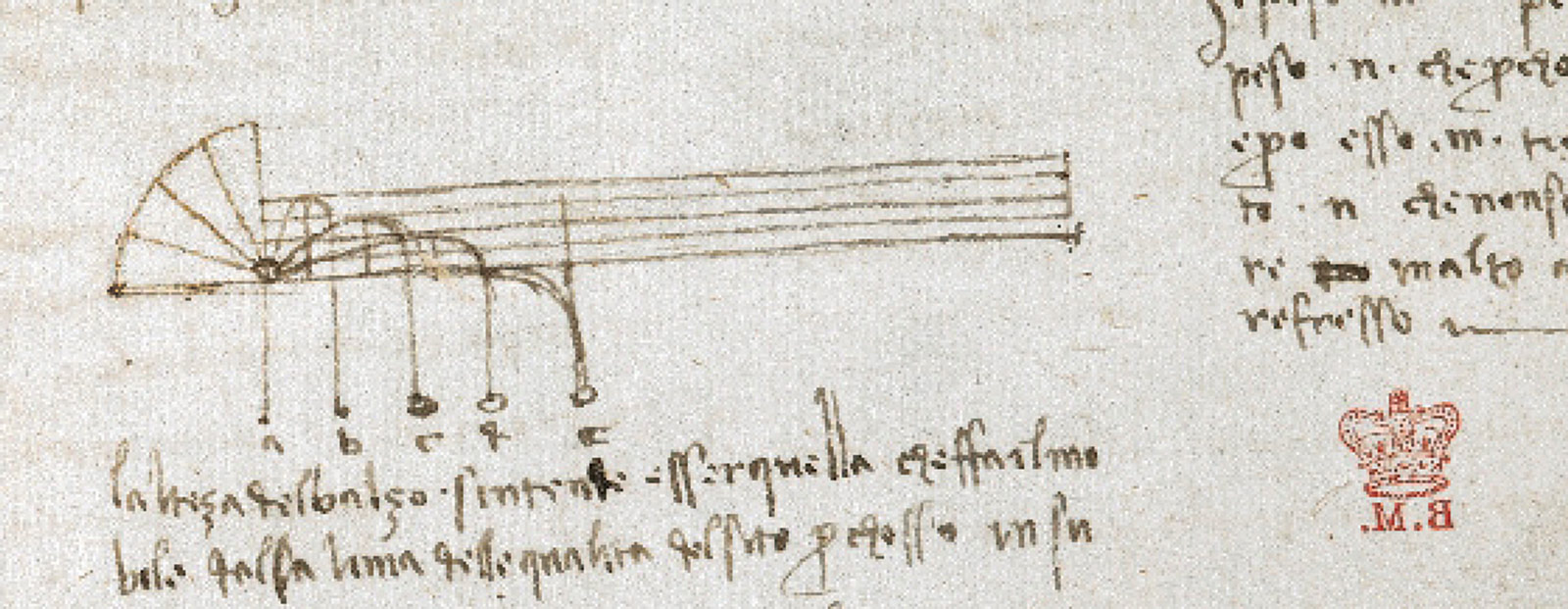
Figure 5. Objects thrown at different angles. The image has been mirrored for ease of understanding (Codex Arundel 92v).

Simply by inspecting Figure 4 and the other pages that Leonardo devoted to this problem, it is clear that he was interested in a simpler geometrical problem: two things that start moving from the same point at the same constant speed but in perpendicular directions will have trajectories that define the two legs of an isosceles right triangle. And the trivial corollary is that if the velocities are different, the triangle will not be isosceles. Da Vinci draws examples of each of these cases and explains how this can be used to estimate the speed of the clouds.

If Leonardo really thought that the particles were following the beautiful parabolic trajectories shown in Figure 3, why didn’t he draw them that way rather than drawing, as he did, vertical lines of no clear meaning? GRN never comment on this obvious weakness in their claim.

Leonardo’s Model?

The next section in GRN’s article is truly strange. In what seems like a misguided attempt to perform a quantitative validation of Leonardo’s ideas on gravity, they make extraordinary assumptions and take huge leaps of faith. They interpret the line in Figure 4 labeled “equation of movement” (it can also be translated as “balanced movement”) as meaning that this figure encodes the actual physical equation of movement. After observing that Leonardo seemed to have bisected the axes, they decide that “presumably, the distance between consecutive bisecting locations represents the distance the object traveled during a fixed time step,” although Leonardo says nothing of the sort. He very clearly says that these bisections represent possible speeds of the cloud, relative to the speed of the hail. According to the supplementary materials provided by GRN, it seems that they came up with “Leonardo’s model” for gravity acceleration by looking at the figures, which may explain their misunderstanding.

GRN claim that “Leonardo’s model” is given by the formula: z(t) ∝ 2(t-1)n, where z is the vertical location of the object, t is time, n is the number of bisections, and ∝ means “proportional to.” It is a strange mixture of a discrete description in terms of bisections (n) and a continuous one in time (t). They recognize that this model is incorrect, but after a few additional assumptions which I will not discuss here, they realize that it is not as bad as it might seem initially. In fact, they say that in certain circumstances it is quite good. They write: “Leonardo’s gravitational constant is 0.9774 (95 percent confidence interval, 0.8535, 1.101), which is close to the nondimensional gravity of 1. These two observations suggest that Leonardo’s model of natural motion, while imperfect, was an accurate representation of his observation of falling objects.”

I don’t think this section requires detailed commentary. GRN start with their wrong interpretation of Leonardo’s manuscripts, invent a model based on what they think a figure means, make some unsupported assumptions, and end up with something that has nothing to do with what Leonardo might have had in mind. One could imagine that they wanted to end their article with some hard numerical results, and they distorted Leonardo’s meaning until it yielded something they could use.

This article appeared in Skeptic magazine 28.3
Buy print edition
Buy digital edition
Subscribe to print edition
Subscribe to digital edition
Download our app

There is, however, an additional point I would like to mention. The model they attribute to Leonardo is invalid for times close to zero (ironically, the only ones for which air drag is insignificant). The plot of z against t that they show in their article and in the supplementary materials does not begin at the origin. The object starts falling only after it is already eight percent of its way down!

* * *

As we have seen, there is no basis to believe that Leonardo da Vinci, genius though he undoubtedly was, had a knowledge of gravity ahead of his time, much less at the level of Newton or Einstein. Every year, thousands of articles are written with the only intention of entertaining casual readers. Their flaws are obvious to most knowledgeable readers. However, this article was published in a peer-reviewed journal by a well-known academic institution. The authors claim to have studied the topic scientifically and their conclusions are not easy to dismiss. One must dig into Leonardo’s large corpus of manuscripts to be able to properly analyze their claims, and few are willing or have the language skills to do so. I have tried my best to examine GRN’s claims carefully. After looking at all the evidence, I remain unconvinced.

Leonardo da Vinci was one of the greatest minds in history. He is unrivaled in having made significant contributions to both science and the arts. There is simply no need for GRN’s hyperbole that Leonardo was a genius who foresaw relativity theory centuries ahead of his time. Their claim is not supported by any fair reading of the original manuscripts. Rather, their paper is a generator of disinformation that has helped to decrease the already too low signal-to-noise ratio in public conversations about science.