
(Image by Ani Aharonian with Daniel Loxton.)
A popular YouTube channel called Numberphile has published a video in which they claim to have a good strategy for winning at Rock, Paper, Scissors, gleaned from a paper on the topic. The video was only posted on January 27th, but it has already been viewed well over a half million times and is popping up in blog posts at popular sites. It’s got some cute animation and the material is presented by a charming mathematician named Hannah Fry who is clearly no dummy.
But several statements she made bothered me and I found the whole thing a confusing jumble when it came to presenting the findings of the paper, so I read the paper myself, did some additional research, and found what I think are some nontrivial problems with the way the paper has been interpreted. The paper was published online nearly a year ago and has been covered on dozens of academic review, popular news, and other websites, at least one of which is likely the source of what Fry presents. Reports range in quality from getting the research completely wrong to a rather good explanation with a ridiculously wrong title.
Nearly every report of this paper got the most crucial detail wrong.
Despite the mess, the Numberphile video gets the most important points correct. However, a critique of it and other sources provides an opportunity to talk about some interesting psychological phenomena. Some readers may think my criticisms minor, but I hope you will all agree that it is a good lesson in critical thinking to parse them out.
Before reading further, watch the video, below. I will wait.
tap tap tap…
Okay, now that you’ve watched the video, let’s talk about Rock, Paper, Scissors.
Fair warning: this may get a little brain-twisty.
The Study’s Purpose and Prescriptive verses Normative Theory
I first want to note something: the purpose of the paper is not to show how to win the game. The purpose of the paper is to describe how people play it. Specifically, the paper examines the dynamics of the decisions people make given outcomes of previous trials. The authors performed model fits to determine if the Nash Equilibrium model could explain human behavior in this context better than a bounded rationality model (more on those later).
In other words, this paper did not set out to determine the optimal decisions, something psychologists call prescriptive theory. It is instead about describing the decisions people tend to make and how–normative theory. Of course, the latter can inform the former as you will see, and so it is not abnormal to spin findings as prescriptive. It is also sometimes more interesting and I am sure that is why virtually every site discussed the research as if it was all about winning at Roshambo, just as Numberphile does.
But in this case, the conclusions they draw are problematic, demonstrating why the difference between these two approaches is not trivial.
The Game
In the video Fry initially breezes through a confusing description of the game and its possible outcomes. Her description appears correct, but only if you are following along with the fact that she has listed possible outcomes, which will allow you to understand what she means by “each strategy wins once and loses once”. She does not differentiate a single game from a set of games–a distinction which I believe is important to understanding the concepts presented.
Let me take a shot at a more clear explanation. Some of this will be important later, so don’t skip this just because you know the game.
Rock, Paper, Scissors is a game in which two players each choose from one of three items, a rock, paper, or scissors. They present their choices at the same time using symbolic hand positions. The winner is decided by comparing the choices: rock beats scissors, scissors beats paper, paper beats rock. If you list all of the possible scenarios and outcomes, you will find that each choice offers one way to win, one way to lose, and one way to tie.
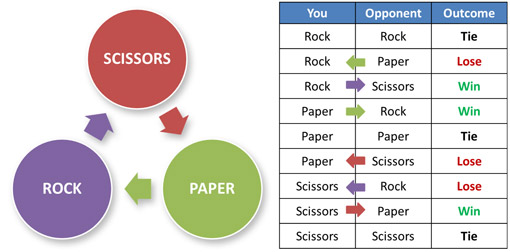
In Rock, Paper, Scissors, rock beats scissors, scissors beats paper, and paper beats rock. (Image by Barbara Drescher.)
So, given that each person chooses from the same three options, outcomes for each choice are equiprobable with a 1/3rd chance of winning, in theory.
The game can be played once or hundreds of times, but each game (or “trial”) is independent from the previous, in theory.
In Theory
Fry appears to make a classic mistake in her description and when she identifies the best strategy for playing a computer. It is an understandable and very human error that has no real effect on the outcome of the game, but one worth discussing. Initially, she correctly describes the basic game saying, “It looks like there is no strategy you can use to win…”, but she contradicts that statement immediately by saying this:
So, really, all you can do is play each strategy with equal probability, a third, a third, a third. Now if you were playing against a computer who is choosing these perfectly randomly, then that would be the best thing for you to do–is just to pick each strategy with equal probability.
Since one cannot “pick with probability” I assume that she means to distribute one’s choices evenly (e.g., in 90 trials, 30 will be rock, 30 paper, 30 scissors). This suggestion is a strategy. You cannot simultaneously believe there is no strategy AND that distributing your choices evenly is the best strategy. That’s a bit like praying when you don’t believe in God.
Anyway, distributing one’s choices evenly is not “the best” strategy. Psychologists call this behavior probability matching–in games such as these people tend to make decisions which match the proportion of responses with the portion they expect a random distribution to produce. For example, people asked to bet on a series of 10 coin flips tend to bet on “heads” 5 times and “tails” 5 times.
Again, this is never an optimal strategy, which makes it interesting behavior to study. Probability matching is sometimes related to a failure to recognize the independence of trials (you may have heard of a version of this called Gambler’s Fallacy). For example, if a coin comes up “heads” three times in a row, most people will bet on “tails” for the next trial, feeling that “tails” is due to hit. However, the probabilities do not change from trial to trial, so this strategy does not increase one’s odds of winning. In the case of Rock, Paper, Scissors, if each trial is independent, we could see “rock” come up 90 times in a set of 90 trials. It’s highly unlikely, but it’s possible.
Now, computers can be programmed to distribute choices equally within a finite set of trials (e.g., so that it chooses each option 30 times in 90 trials). This would give a player some control over the odds. However, probability matching is still not optimal. Since you have no idea which trials the computer is going to produce “scissors”, you cannot match your choice to each trial. But, because you know that at least 1/3rd of the trials will be “scissors”, you would be guaranteed to win 1/3rd of the trials if you chose “rock” each time. The best strategy would be to keep track of the trials and recalculate the odds after each trial. If, for example, “rock” comes up on the first trial, the probability of it coming up on the second trial is slightly lower than the probability of “paper” or “scissors”*, so your best choice is “scissors”. This strategy will give you a slight edge. If you use Fry’s strategy, you have the same chances as choosing at random: you would expect to win about 1/3rd of the trials, but you could win all of them or none of them.
In a set of truly independent trials of Rock, Paper, Scissors, there is no best strategy.
All of that said, if you are playing this game with a computer, it is most likely that it is programmed to choose from the three options randomly for each trial, making each independent. Although probability matching is no worse than other strategies, it is not “the best” strategy. In a set of truly independent trials of Rock, Paper, Scissors, there is no best strategy.
In Practice
In practice, there is more to Rock, Paper, Scissors than basic probabilities because the game is played by human beings. This makes the probability of winning given a particular action much more complicated. In order to determine these probabilities, we need information about how people play. Do people tend to throw “rock” more often than “paper”? How do people play when they think about how their opponent will play? Determining the best strategy can get really complicated really fast.
The study of how people behave in competitive situations is a mixture of math and psychology known as game theory, and game theory is what the study is actually about.
The Study
The study (it is not an experiment in the strict sense of the word) involved 354 students who were placed into 59 groups of six**. They called these groups “populations”. The students played 300 rounds of Rock, Paper, Scissors, changing partners within their group of six after each round (or trial). They were paid for each win at the end of the session.
The analysis involved coding behavior mathematically so that they could operationally define shifts in choice in terms of cycles around the triangle. You will notice in the diagram here that going from one item to the item it beats means moving in a clockwise direction: rock, scissors, paper, rock… Going from an item to the item that beats it would mean moving in a counter-clockwise direction: rock, paper, scissors, rock…
As I described, the authors were interested in whether the Nash Equilibrium [NE] model could fully explain behavior. The authors state that an NE model would predict that players will try to avoid being exploited by their opponents by remaining unpredictable. They expect players following this strategy to choose each option at about the same rate as each other option (an equal distribution), but not in a cyclical manner. In other words, one would have to move clockwise at times, counter-clockwise at times, and repeat at times. Over a large number of trials, movement would average to zero.
What They Found
They found quite a few things, but only these are relevant:
When they examined all trials they found that, although individual participants preferred “rock” to “paper” and “paper” over “scissors”, the differences were small at ~36%, ~33%, and ~32%, respectively. The authors described this distribution as consistent with NE strategy. Indeed, a rough Chi-Square shows that these values do not differ much from what we would expect to find in a random distribution. This means that we cannot conclude that people, in general, are more likely to play “rock” than the other choices.
When they examined populations (groups of six), they found persistent counter-clockwise cycling (i.e., rock to paper to scissors and so on) in all populations. This cannot be explained by the NE model.
When examining consecutive trials, they discovered that the outcome of one trial affected the choices individuals made on the next trial such that:
- Winners tended to repeat the same choice.
- Losers tended to move clockwise (i.e. rock to scissors to paper and so on).
This follows a well-known pattern called a “win-stay, lose-shift” strategy, but with a specific direction to the shift. This pattern is called a conditional response pattern because a choice depends on the outcome of the previous trial.
What Does This All Mean?
If there are patterns to individual behavior, then we might be able to exploit this by predicting what our opponent will play next. This is what Fry and most websites focused on.
However, nearly every website that talked about the findings as losers moving clockwise, including MIT, BBC, Business Insider, The Washington Post, and IFLS, got the most important detail wrong. They described “clockwise” as the direction the name takes (Rock, Paper, Scissors). However, take a look at the illustration, which is similar to the diagram provided in the paper. It aligns with the description in the paper which reads:
…to shift action either counter-clockwise (i.e., R → P, P → S, S → R, see Fig. 1B) or clockwise (R → S, S → P, P → R).
Many reprinted the illustrations, directly contradicting them in their text. So when they said that losers shifted clockwise, they suggested the wrong direction. This mistake is even repeated in a video by Buzzfeed. That’s kind of an important detail if you’re going to use that information to determine your move. How did nobody catch this?
In the Numberphile video, Fry gives fine advice, but in a confusing manner. She draws an illustration that is a mirror image of the one in the paper, repeating the problem of reversing the direction, then uses the word “backwards” to describe moving in the direction of the arrows (she likely meant backwards relative to the name–scissors, paper, rock). She manages to avoid repeating the mistake the others made by failing to describe how losers behaved in the study (she says they shifted, but not which direction). She gives the following advice, which is correct:
- If you lose, the winner will probably play the same thing again, so your best bet is to play what beats that. (Fry fails to note that this is exactly what losers did in the study.)
- If you win, anticipate that the loser will play the thing that will beat what you just played.
And she stops there.
So she has advised winners to anticipate what losers will do based on what losers think that winners will do, but she advises losers to anticipate what winners will do without considering what winners might know about what losers are likely to do. Of course, if both winners and losers do this, it begins to look like this scene in The Princess Bride:
Man in Black: All right. Where is the poison? The battle of wits has begun. It ends when you decide and we both drink, and find out who is right… and who is dead.
Vizzini: But it’s so simple. All I have to do is divine from what I know of you: are you the sort of man who would put the poison into his own goblet or his enemy’s? Now, a clever man would put the poison into his own goblet, because he would know that only a great fool would reach for what he was given. I am not a great fool, so I can clearly not choose the wine in front of you. But you must have known I was not a great fool, you would have counted on it, so I can clearly not choose the wine in front of me.
Man in Black: You’ve made your decision then?
Vizzini: Not remotely. Because iocane comes from Australia, as everyone knows, and Australia is entirely peopled with criminals, and criminals are used to having people not trust them, as you are not trusted by me, so I can clearly not choose the wine in front of you.
Man in Black: Truly, you have a dizzying intellect.
Vizzini: Wait till I get going! Now, where was I?
Man in Black: Australia.
Vizzini: Yes, Australia. And you must have suspected I would have known the powder’s origin, so I can clearly not choose the wine in front of me.
Man in Black: You’re just stalling now.
Vizzini: You’d like to think that, wouldn’t you? You’ve beaten my giant, which means you’re exceptionally strong, so you could’ve put the poison in your own goblet, trusting on your strength to save you, so I can clearly not choose the wine in front of you. But, you’ve also bested my Spaniard, which means you must have studied, and in studying you must have learned that man is mortal, so you would have put the poison as far from yourself as possible, so I can clearly not choose the wine in front of me.
Apply that to Rock, Paper, Scissors and you can see how determining the best strategy can get really complicated really fast.
If you lose and you know that the winner knows that you are likely to shift clockwise, then you should consider that and move counter-clockwise. And if you win, you should anticipate that the loser will know that you know that they will shift clockwise and that they will instead shift counter-clockwise, so you should then shift counter-clockwise. And if you lose and you know that the winner knows that you know that they are likely to stay, then you should move clockwise. And they know that you know that they know that you know… And so on, putting you right back where you started, with no ability to predict what your opponent will do.
*sigh*
Some websites mention this problem, but I found very few who noted the more important problem with the advice: it’s an untested hypothesis.
The researchers noted that the win-stay, lose-shift strategy they observed has the potential to produce higher payoffs than the NE strategy of equal distributions. However, they also noted that this hypothesis was not tested. This did not stop at least one site from calling it “scientifically proven”.
Furthermore, it is important to understand the difference between statistical significance and practical significance. These findings came from over 100,000 data points. The differences are statistically significant, but that does not mean that the same effect can be seen on a small scale like a best-two-out-of-three scenario. And of course it cannot help you at all in a single game.
Okay, so it’s untested, but it’s based on good research, right? Well, yes, but let’s not forget how the study was conducted. They found this pattern of behavior in a very specific context. This was not pairs of people playing many rounds of the game with the same partner. This was groups of six who shuffled partners after every round. That is not a typical Rock, Paper, Scissors scenario. Also keep in mind that this study was actually about collective behavior (the populations showed a persistent counter-clockwise cycling pattern). We have no idea if this behavior would also occur in typical game play.
So What Should You Do?
Even for a single game the evidence is frustrating. Fry says (in the extra footage video) that “most people play rock” because “it’s really powerful”. However, that’s not what the empirical evidence says. Yes, in the study people were more likely to choose rock, but the difference was not statistically significant. Something may be statistically significant without being practically significant, but not the other way around. If it is not statistically significant, we cannot generalize outside of the study.
In other words, the evidence says that people do not choose “rock” more often than “paper” or “scissors”.
So after all of that, what should you do?
In the end I think Joshua said it best:
The only winning move is not to play.
*If you are unsure why, remember that in 90 trials there must be 30 of each item, so the probability of the first trial coming up “rock” is 30 in 90, or 1 in 3. If the first trial is “rock”, only 29 of the remaining 89 trials will be “rock”, but there will be 30 each of “paper” and “scissors”. Therefore, the probability of “rock” in the second trial is 29 in 89, which is less than 1 in 3. The probability of getting “rock” on the second trial depends on the outcome of the first trial.
**They started with 360 in 60 groups, but one group’s behavior was so unusual that the data were thrown out.










This analysis takes a considerable amount of time to formulate. One has the count of three as limiter to brain function. This likely gives ‘paper’ the odds on favorite, under stress, because of it’s ease of hand construction in a pinch. The next time you’re asked to play, at some point throw in a fourth object–water–wiggle your fingers. Water rusts scissors, erodes rock, and mushes paper.
There are rock-paper-scissors programming contests.
This one shows the code for all submissions.
http://www.rpscontest.com
If you program your bot to choose randomly, it’ll win half of its matches. But if the opponents have some non-random strategy, and you program your bot to exploit it, then your bot will have a non-random strategy that the opponents can exploit. And some bots perform a lot better than others.
Previous contests had a mini-bot competition for small programs with relatively few lines of code.
This one-liner by Johannes Fuernkranz was the winner in the “most for the least” category:
return((*opp_history?opp_history[random()%*opp_history+1]+1:random())%3);
Let me see if I can translate that one-liner into English.
Suppose the cycle is rock to paper to scissors to rock.
If the opponent’s last choice was a rock, return a random selection.
Otherwise:
If the opponent threw paper, take what it threw one throw ago, and cycle by one.
If the opponent threw scissors, randomly pick what it threw one OR two throws ago, and cycle by one.
Ii think it is appropriate for Barbara to talk about the video, and the discussion includes a major point: how much thinking does your opponent do?
I appreciate her pointing out that changing partners after every trial makes the whole “experiment” meaningless except for the frequency of each choice.
A good example of the sort of thing I was complaining about is Barbara’s sentence, “Since one cannot “pick with probability” I assume that she means to distribute one’s choices evenly”. Pointless pedantry illuminating no substantive point whatsoever.
I don’t have a problem with “pick with probability”, and it is disingenious of Barbara to say that she “assumes” Fry means “to distribute one’s choices evenly” when it is utterly transparent that this is what she is saying and assumption has nothing to do with it.
Fry’s persistent use of the term “strategy” where she means “option” *is* worthy of a parenthetical note, but it is not worth dwelling on. It indicates that Fry could have taken more editorial care when preparing her introduction, nothing more.
Adrian Morgan, you have twice made your complaint yet you have added nothing of value to Barbara’s article or to the discussion.
Adrian’s comment clarified that “strategy” simply meant “option” in the video. Fortunately, I read his comment before watching the video or reading the article. That’s what much of the fuss is about.
Thanks for your reply, Max. Having spent decades studying psychology and cognitive neuroscience, I fully understand why Barbara wrote “Nearly every report of this paper got the most crucial detail wrong.” and I’m very pleased that she has taken the time to provide us with a detailed explanation of not just the video, but the underlying failures in human cognition and rationality.
To describe Barbara’s article as “pedantic nitpicking of Fry’s syntax” is totally missing the point of both the article and scientific skepticism in general.
This is not one of the better articles on Insight. The pedantic nitpicking of Fry’s syntax goes too far and detracts from the substantive issues.